Solving The Witness with Z3 (Part 1)

Aug 25 2022

The Witness (2016) is a fantastic puzzle game created by Jonathan Blow and Thekla Inc. The game is best experienced blind and this post will be riddled with spoilers, so if you have any intention of playing the game, stop reading now.

The puzzles in the game are based on one simple mechanic: drawing a line through a grid. The line starts at a source, travels along edges, passes through intersections, and eventually ends at an exit without crossing over itself.

The rules are never explained in English (the player discovers them through trial and error), so the terms I’m using are arbitrary. Other terminology will be introduced as we go.

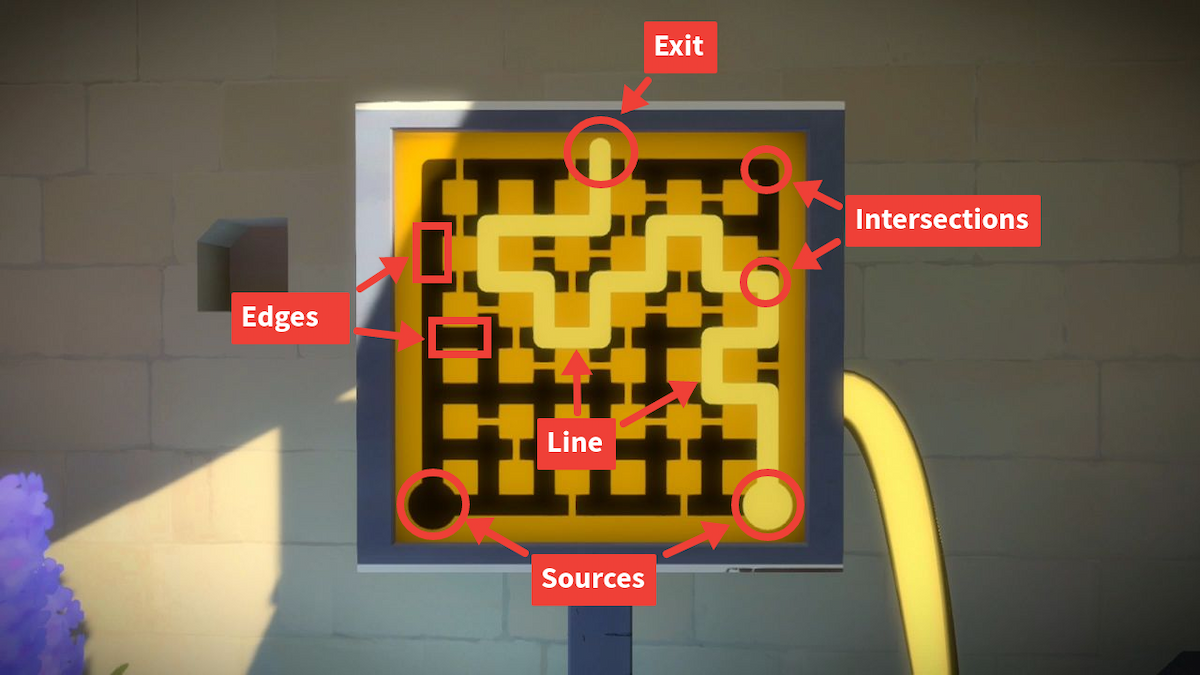
If that were the full story, this would be a much shorter post. In addition, various symbols are introduced throughout the game which constrain the line in unusual ways. For example, the line must pass through all the small hexagonal dots, while also separating squares of different colours.

A puzzle with hexagonal dots and squares.

In this series, I will explain how to build an efficient puzzle solver for The Witness using Z3 Prover and Rust. This first part will focus on the line and hexagonal dots.

Source code: https://github.com/Bickio/the-witness-solver

Puzzle format

Before we start solving puzzles, we need a way to describe and store puzzles. For this series, we will only be dealing with grid-based puzzles, so we can describe positions as 2d coordinates.

#[derive(Debug, Clone, PartialEq)]
pub struct Pos {
    pub x: u32,
    pub y: u32,
}

Intersections are simply positions on the grid. Edges can be described by their top-left position and then either horizontal or vertical.

#[derive(Debug, Clone, PartialEq)]
pub struct Edge {
    pub pos: Pos,
    pub dir: EdgeDirection,
}

#[derive(Debug, Clone, PartialEq)]
pub enum EdgeDirection {
    Horizontal,
    Vertical,
}

Placement of all other puzzle elements falls into two categories:

On the grid (either an intersection or an edge)
In a cell (the square areas surrounded by four edges)

The four puzzle elements we will be looking at in this post are:

Sources
Exits
Broken edges/intersections
Dots

All of these lie on the grid, on both edges and intersections. If you’ve played the game you might not agree with that statement, but edges with sources/exits and broken intersections, while uncommon, do exist. Elements which lie in cells will be the subject of future posts.

The final thing to add is the width and height of the puzzle.

#[derive(Debug, Clone, PartialEq)]
pub struct Puzzle {
    pub width: u32,
    pub height: u32,
    pub sources: Vec<IntersectionOrEdge>,
    pub exits: Vec<IntersectionOrEdge>,
    pub broken: Vec<IntersectionOrEdge>,
    pub dots: Vec<IntersectionOrEdge>,
}

#[derive(Debug, Clone, PartialEq)]
pub enum IntersectionOrEdge {
    Intersection(Pos),
    Edge(Edge),
}

Modelling a solution

Now that we have a format for describing puzzles, we can model what a solution should look like. Then, we will add constraints to ensure that the solution is correct.

Every edge and intersection will be a node. Each edge node is adjacent to two intersection nodes, and each intersection node is adjacent to up to four edge nodes.

Each node holds two types of variables:

Given variables
Solved variables

Given variable values are derived from our puzzle specifications, while solved variable values are left to Z3 to determine.

For now, we will have three solved variables:

has_line
source_used
exit_used

has_line represents whether the line passes through the node. source_used and exit_used are true if that node is used as the source or exit. These are distinct from has_line because the line may pass through a source/exit without terminating there.

#[derive(Debug, Clone)]
struct Node<'ctx> {
    broken: bool,
    source: bool,
    exit: bool,
    dot: bool,
    has_line: z3::ast::Bool<'ctx>,
    source_used: z3::ast::Bool<'ctx>,
    exit_used: z3::ast::Bool<'ctx>,
}

These nodes will be stored in a PuzzleModel struct, in a way we can easily retrieve the ones we want. There are many ways of achieving this, but I chose to store them in 2d vectors, with getters to retrieve them using the puzzle format types.

#[derive(Debug)]
struct PuzzleModel<'ctx> {
    ctx: &'ctx z3::Context,
    width: u32,
    height: u32,
    intersections: Vec<Vec<Node<'ctx>>>,
    horizontal_edges: Vec<Vec<Node<'ctx>>>,
    vertical_edges: Vec<Vec<Node<'ctx>>>,
}

impl<'ctx> PuzzleModel<'ctx> {
    fn intersection(&self, pos: &puzzle::Pos) -> &Node<'ctx> {...}
    fn intersection_mut(&mut self, pos: &puzzle::Pos) -> &mut Node<'ctx> {...}
    fn edge(&self, edge: &puzzle::Edge) -> &Node<'ctx> {...}
    fn edge_mut(&mut self, edge: &puzzle::Edge) -> &mut Node<'ctx> {...}
    fn node(&self, intersection_or_edge: &IntersectionOrEdge) -> &Node<'ctx> {...}
    fn node_mut(&mut self, intersection_or_edge: &IntersectionOrEdge) -> &mut Node<'ctx> {...}
    fn adjacent(&self, intersection_or_edge: &IntersectionOrEdge) -> Vec<IntersectionOrEdge> {...}
    fn adjacent_nodes(&self, intersection_or_edge: &IntersectionOrEdge) -> Vec<&Node> {...}
    fn adjacent_edges(&self, pos: &puzzle::Pos) -> Vec<puzzle::Edge> {...}
    fn adjacent_intersections(&self, edge: &puzzle::Edge) -> Vec<puzzle::Pos> {...}
    fn from_puzzle(p: &puzzle::Puzzle, ctx: &'ctx z3::Context) -> Self {...}
}

I have left out the implementations for brevity, but you can find them in the github repository for this series.

Adding constraints

Now that we have a model containing our variables, we can place constraints on those variables for Z3 to resolve. The constraints will be added to a z3::Solver object.

    fn constrain(&self, solver: &z3::Solver) {...}
    fn constrain_intersection_or_edge(
        &self,
        solver: &z3::Solver,
        intersection_or_edge: &IntersectionOrEdge,
    ) {...}
    fn constrain_sources_and_exits(
        &self,
        solver: &z3::Solver,
        sources: Vec<IntersectionOrEdge>,
        exits: Vec<IntersectionOrEdge>,
    ) {...}

The constrain method simply calls constrain_intersection_or_edge for each intersection and edge in the puzzle, and then calls constrain_sources_and_exits.

Node constraints

Let’s take a look at constrain_intersection_or_edge first.

First, we enforce the given variables:

The line must not pass through a broken node
A non-source must not be used as a source
A non-exit must not be used as an exit
The line must pass through every dot

fn constrain_intersection_or_edge(...) {
    let node = self.node(intersection_or_edge);
    if node.broken {
        solver.assert(&!&node.has_line);
    }
    if !node.source {
        solver.assert(&!&node.source_used);
    }
    if !node.exit {
        solver.assert(&!&node.exit_used);
    }
    if node.dot {
        solver.assert(&node.has_line);
    }
    ...
}

Next we build some helper expressions for the number of adjacent nodes. These variables do not hold concrete values yet; the values will be determined later by Z3. Instead, they hold an abstract syntax tree (AST) of operations on Z3 variables.

fn constrain_intersection_or_edge(...) {
    ...
    let adjacent_nodes = self.adjacent_nodes(intersection_or_edge);
    let adjacent_nodes_with_line = adjacent_nodes
        .iter()
        .map(|adj| (&adj.has_line, 1))
        .collect::<Vec<_>>();
    let zero_adjacent_lines = z3::ast::Bool::pb_eq(&self.ctx, &adjacent_nodes_with_line, 0);
    let one_adjacent_line = z3::ast::Bool::pb_eq(&self.ctx, &adjacent_nodes_with_line, 1);
    let two_adjacent_lines = z3::ast::Bool::pb_eq(&self.ctx, &adjacent_nodes_with_line, 2);

    let is_source_or_exit = &node.exit_used | &node.source_used;
    let is_source_and_exit = &node.exit_used & &node.source_used;
    ...
}

pb_eq deserves a little explanation. It takes a sequence of (z3::ast::Bool, int) pairs, and adds up the ints with true bools. It then returns true if the total matches the second argument k. In this example, all the ints are set to 1, so it effectively checks whether the number of true bools is 0, 1 or 2 respectively.

Finally, we check that the line is continuous, and starts/ends at a source/exit. There are four valid states for a node:

The node is not part of the line at all
The line passes through the node
The line starts or ends at the node
The starts and ends at the node

fn constrain_intersection_or_edge(...) {
    ...
    let valid_not_in_line = !&node.has_line & !&is_source_or_exit;
    let valid_middle_of_line = &node.has_line & !&is_source_or_exit & &two_adjacent_lines;
    let valid_end_of_line = &node.has_line & &is_source_or_exit & &one_adjacent_line;
    let valid_entire_line = &node.has_line & &is_source_and_exit & &zero_adjacent_lines;
    solver.assert(
        &(valid_not_in_line | valid_middle_of_line | valid_end_of_line | valid_entire_line),
    );
}

Don’t get confused by all the ampersands! Some denote rust references, others logical AND.

Source/exit constraints

Under the rules above, any puzzle without dots is solvable: just don’t draw a line at all! Clearly this is not intended, so we need to ensure that there is exactly one line drawn. The simplest way to do this is to check that we have used exactly one source and one exit.

fn constrain_sources_and_exits(
    &self,
    solver: &z3::Solver,
    sources: Vec<IntersectionOrEdge>,
    exits: Vec<IntersectionOrEdge>,
) {
    solver.assert(&z3::ast::Bool::pb_eq(
        self.ctx,
        &sources
            .iter()
            .map(|source| (&self.node(source).source_used, 1))
            .collect::<Vec<_>>(),
        1,
    ));
    solver.assert(&z3::ast::Bool::pb_eq(
        self.ctx,
        &exits
            .iter()
            .map(|exit| (&self.node(exit).exit_used, 1))
            .collect::<Vec<_>>(),
        1,
    ));
}

This logic will change in a future post where we account for symmetry puzzles with two symmetric lines.

Final touches

Finally, we wrap this all in a solve function which sets up Z3 to work its magic. If Z3 finds a model which meets all of the constraints, we extract the line from the model (see repo for implementation).

If there is no model which meets the constraints, we simply return None. Z3 is able to logically prove that the constraints cannot be satisfied, so this could be extended to show a chain of reasoning as to why a puzzle is impossible. However, that’s well beyond the scope of this series!

pub fn solve(puzzle: &puzzle::Puzzle) -> Option<Vec<IntersectionOrEdge>> {
    let cfg = z3::Config::new();
    let ctx = z3::Context::new(&cfg);
    let puzzle_model = PuzzleModel::from_puzzle(puzzle, &ctx);
    let solver = z3::Solver::new(&ctx);
    puzzle_model.constrain(&solver);
    match solver.check() {
        z3::SatResult::Sat => {
            let model = solver.get_model().unwrap();
            Some(puzzle_model.extract_line(&model))
        }
        _ => None,
    }
}

What’s next?

There’s lots more to implement before we have a complete solver. Keep an eye out for Part 2 where I will be working on coloured square and sun symbols, and formalising the intuition behind cells and cell regions.

Two puzzles with coloured squares and suns

If you found this post interesting or you have questions, let me know in the comments. This is my first foray into blogging, so feedback is very much appreciated!

Solving The Witness with Z3 (Part 2).