Solving The Witness with Z3 (Part 2)

Read the first part here: Solving The Witness with Z3 (Part 1)

Source code: https://github.com/Bickio/the-witness-solver

SPOILER WARNING: The Witness is best experienced blind. If you have any intention of playing the game, stop reading now.

Bug roundup

Before we crack into the new features, I would like to acknowledge a bug. The constraints in the last post allowed for extra loops, separate to the line itself.

Fortunately, fixing this is fairly simple. All we need to do is consecutively number the nodes in the line. At some point in a loop, the numbers cannot continue rising, so it will not satisfy the condition.

The beauty of this solution is that it doesn’t matter where you start or what number you start from, it simply has to be a consecutive sequence. This means we can easily model it at the local level.

We add a Z3 Int variable to each node:

struct Node<'ctx> {
    ...
    line_index: z3::ast::Int<'ctx>,
    ...
}

And implement our local constraint on a node in the middle of a line:

For every pair A and B of nodes adjacent to the current node C.

If both A and B are part of the line, then either:

• A’s line index == C - 1 and B’s line index == C + 1, OR
• A’s line index == C + 1 and B’s line index == C - 1

fn constrain_intersection_or_edge(...) {
    ...
    let one = z3::ast::Int::from_i64(&self.ctx, 1);
    let consecutive_numbers = adjacent_nodes
        .into_iter()
        .combinations(2)
        .map(|pair| {
            let pair_has_line = &pair[0].has_line & &pair[1].has_line;
            let increasing = &node.line_index._eq(&(&pair[0].line_index - &one))
                & &node.line_index._eq(&(&pair[1].line_index + &one));
            let decreasing = &node.line_index._eq(&(&pair[0].line_index + &one))
                & &node.line_index._eq(&(&pair[1].line_index - &one));
            pair_has_line.implies(&(&increasing | &decreasing))
        })
        .reduce(|acc, condition| acc & condition)
        .unwrap_or(z3::ast::Bool::from_bool(&self.ctx, false));

    ...
    let valid_middle_of_line = ... & &consecutive_numbers;
    ...
}

With that out of the way, let’s move onto some new game rules!

Regions

Most of the remaining puzzle mechanics are based on the following simple idea: The line partitions the grid into separate regions.

In this solution, the four regions have been painted different colours:

Unfortunately, not all simple ideas translate into simple rules. Let’s formalise this a bit.

• The square spaces surrounded by four grid edges are cells

1. Cells belong to exactly one region
2. Adjacent cells not separated by the line must be in the same region
3. Regions must be connected without crossing the line or leaving the grid

Constraints #1 and #2 are trivial to implement, so let’s get that out of the way.

First, we need a way to represent cells, and what region they belong to. This ensures constraint #1 by default.

struct Cell<'ctx> {
    region: z3::ast::Int<'ctx>,
}

struct PuzzleModel<'ctx> {
    ...
    cells: Vec<Vec<Cell<'ctx>>>,
}

Then, we add constraint #2:

fn constrain_regions(...) {
    ...
    for edge in self.edges() {
        let adj_cells = self.adjacent_cells(&edge);
        if adj_cells.len() == 2 {
            let region_a = &self.cell(&adj_cells[0]).region;
            let region_b = &self.cell(&adj_cells[1]).region;
            solver.assert(
                &self
                    .edge(&edge)
                    .has_line
                    .not()
                    .implies(&region_a._eq(region_b)),
            );
        }
    }
}

Constraint #3 is not so straight forward. I considered a few options with little success.

Constraints across the line

Could we simply say: Cells separated by the line must be in different regions? It certainly it seems logical!

In fact, any puzzle with an internal source or exit (i.e. not on the border) must break this rule! In this example, the region containing red squares extends to both sides of the line:

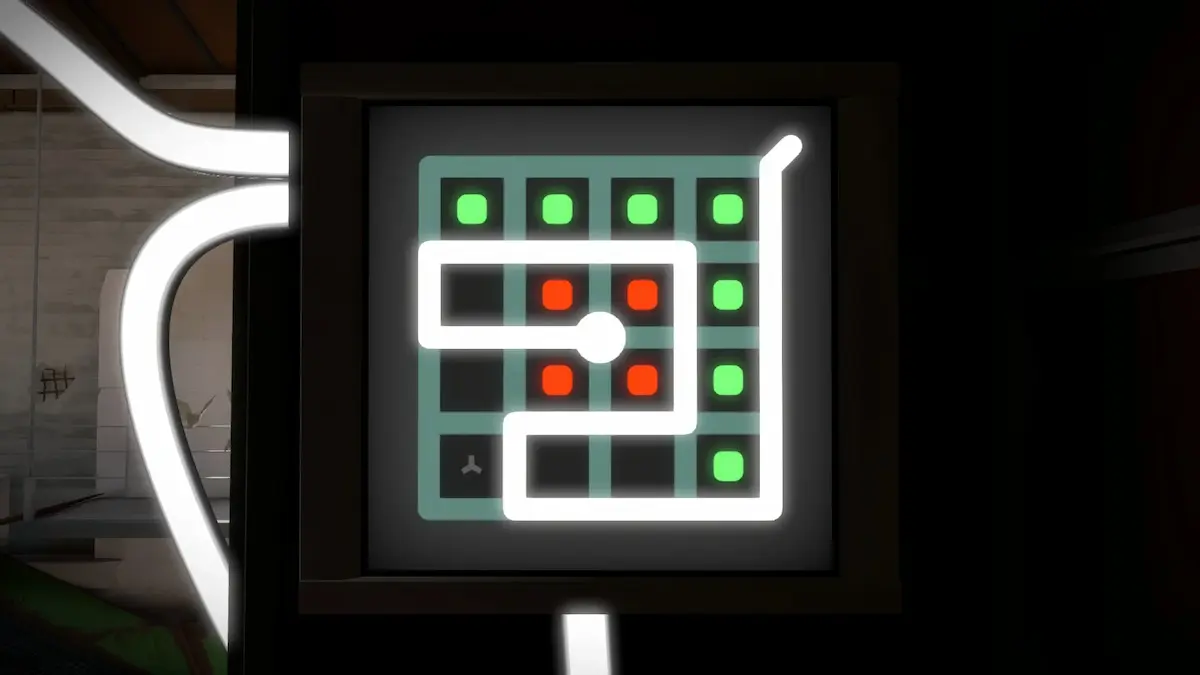
Even ignoring that, we have a bigger problem. This rule alone does not prevent non-touching regions from being incorrectly assigned the same region number!

For example, we could end up with the following regions:

Clearly, this does not meet our requirements.

Number of regions

Here’s an idea: If we knew exactly how many regions there should be, we can easily ensure that we have the right number!

Regions are already described as numbers, so we’d simply have to say that there must be a cell with each number from 0 to N-1!

First, we store the number of regions. This must be a Z3 variable, as ultimately this will be derived from the line.

#[derive(Debug)]
struct PuzzleModel<'ctx> {
    ...
    num_regions: z3::ast::Int<'ctx>,
}

Next, we ensure that every cell has a valid region number: 0 <= R < N

fn constrain_regions(...) {
    ...
    for cell_pos in self.cell_positions() {
        let cell = self.cell(&cell_pos);
        let cell_region = &cell.region;
        solver.assert(&(cell_region.ge(&zero)));
        solver.assert(&(cell_region.lt(&self.num_regions)));
    }

Now for the tricky bit. We need to guarantee that every region has at least one cell. For this, we will use a Z3 ForAll quantifier.

The Z3 variable region will represent an arbitrary region.

    let region = z3::ast::Int::fresh_const(self.ctx, "region");

Then we create expressions:

• valid_region: Whether the region is within a valid range
• cells_in_region: A vec describing whether each cell is in the region

    let valid_region = &region.ge(&zero) & &region.lt(&self.num_regions);
    let cells_in_region: Vec<_> = self
        .cell_positions()
        .iter()
        .map(|pos| self.cell(pos).region._eq(&region))
        .collect();

Finally, we add the constraint that for all possible values of region: if the region number is valid, there must at least one cell in the region.

    solver.assert(&z3::ast::forall_const(
        self.ctx,
        &[&region],
        &[],
        &valid_region.implies(&z3::ast::Bool::pb_ge(
            self.ctx,
            cells_in_region
                .iter()
                .map(|cond| (cond, 1))
                .collect::<Vec<_>>()
                .as_ref(),
            1,
        )),
    ));

So, how many regions should there be?

Let’s consider a simple case, where the line starts and ends on the border of the grid.

If the line never leaves the border, we clearly have only one region. Each time the line crosses the grid, it adds another region.

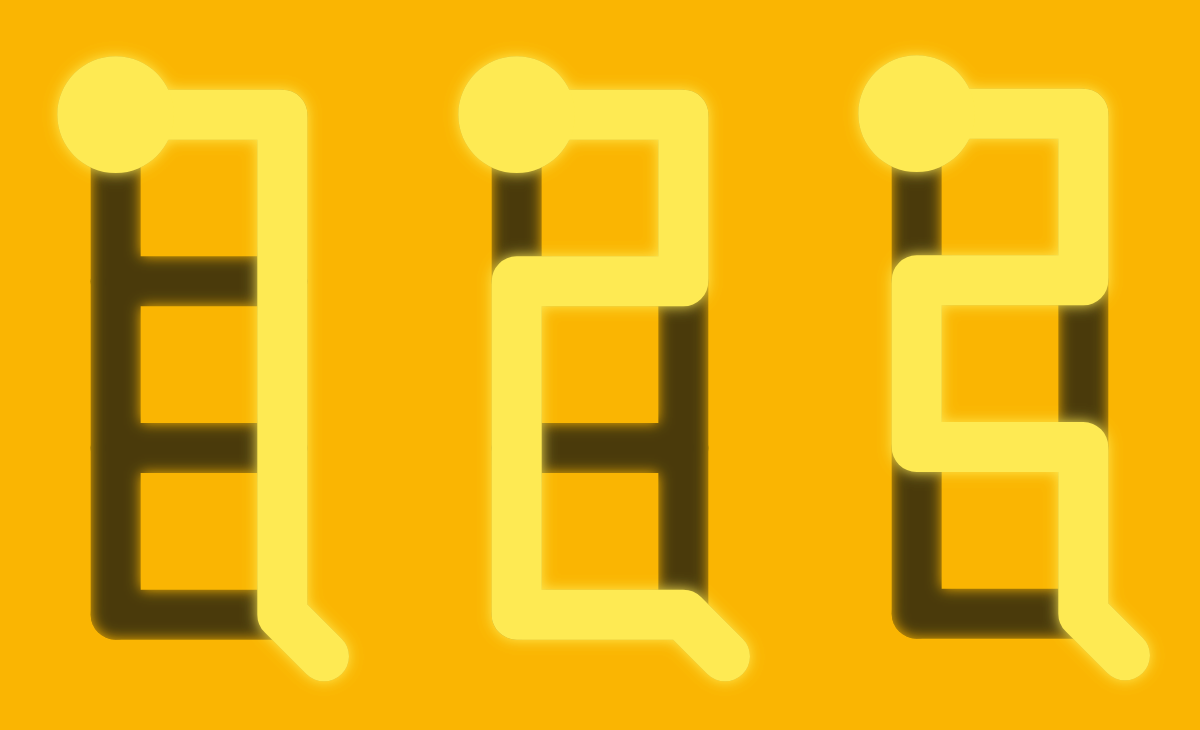
In other words, there is always one more region than the number of times the line completely crosses the grid.

How do we know how many times the line crosses the grid? Each time it crosses, it will pass through two of the following white edges:

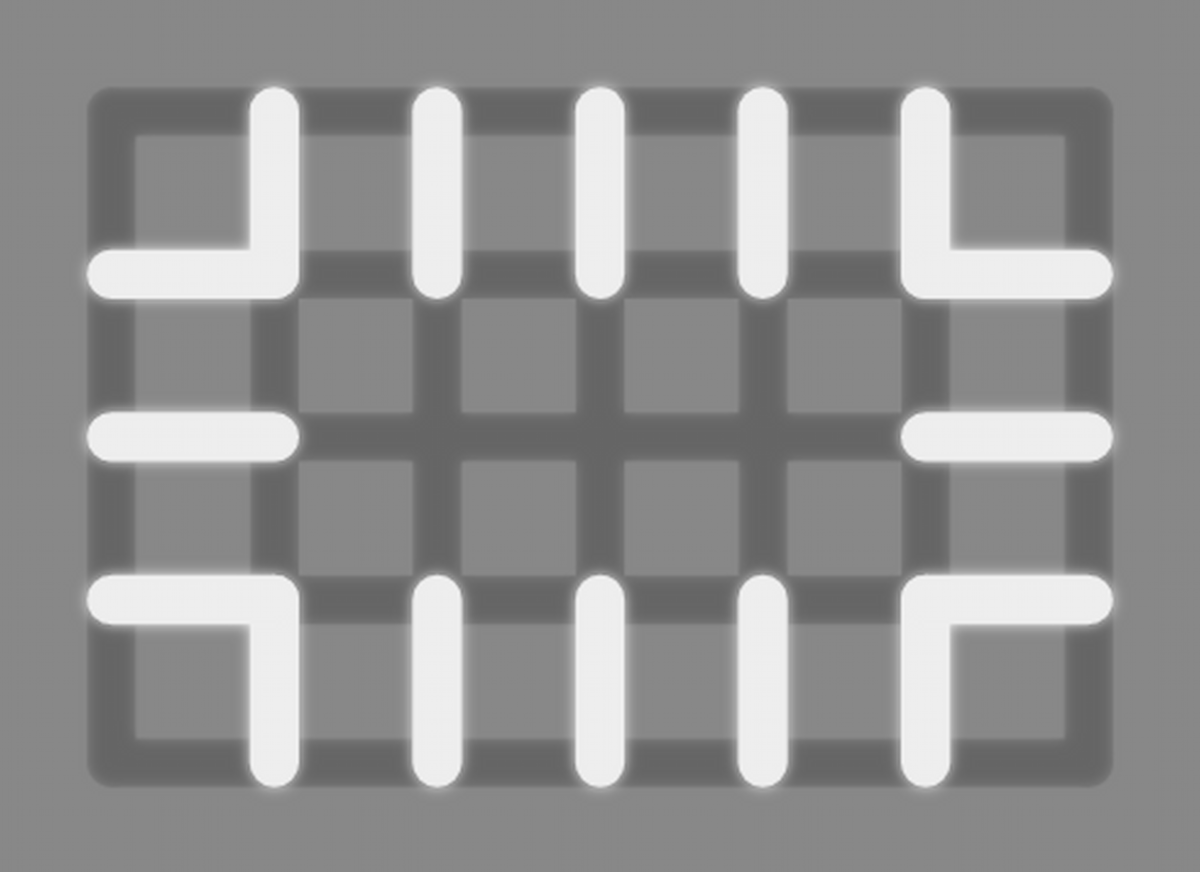
So we can simply count up the number of those edges it passed through, divide by two and add one to get the number of regions.

let edge_lines_from_border = self
    .edges_from_border()
    .iter()
    .map(|edge| self.edge(edge).has_line.ite(&one, &zero))
    .reduce(|accum, num| accum + num)
    .unwrap_or_else(|| z3::ast::Int::from_i64(self.ctx, 0));
let mut num_regions = edge_lines_from_border
    .div(&z3::ast::Int::from_i64(self.ctx, 2))
    + &one;

Internal terminations

The last little detail to consider is internal sources/exits. For each end of the line which is not on the border, the line will pass through one extra highlighted edge. We can simply subtract the number if internal sources/exits from the number of times the line leaves the border to account for this.

let internal_terminations = sources
    .iter()
    .chain(exits.iter())
    .filter(|intersection_or_edge| !self.is_external(intersection_or_edge))
    .map(|intersection_or_edge| self.node(intersection_or_edge))
    .map(|node| (&node.source_used ^ &node.exit_used).ite(&one, &zero))
    .reduce(|accum, num| accum + num)
    .unwrap_or_else(|| z3::ast::Int::from_i64(self.ctx, 0));
...
let mut num_regions = (edge_lines_from_border - internal_terminations)
    .div(&z3::ast::Int::from_i64(self.ctx, 2))
    + &one;

There is one exception to this rule. If the line never touches the border, we may end up with no regions using the previous calculation. The two lines here both create one region, but our calculation would give zero for the first one:

For a puzzle with at least one cell there must be at least one region, so we can simply round any zero up to one.

num_regions = num_regions.le(&zero).ite(&one, &num_regions);

As you may have already realised, puzzles with no cells cannot have regions, so we will only restrict the number of regions if there are cells.

if self.width > 0 && self.height > 0 {
    solver.assert(&self.num_regions._eq(&num_regions));
};

Squares and suns

Constraining regions was almost the entire battle! We’re on the home stretch.

Squares enforce a simple rule: A square must be the same colour as every other square in its region.

The sun rule is equally simple: A sun must be in a region with exactly one other symbol of the same colour.

Let’s crack into the code.

First we need a way of specifying where squares/suns are in the puzzle:

pub struct Puzzle {
    ...
    pub squares: Vec<ColouredSymbol>,
    pub suns: Vec<ColouredSymbol>,
}

#[derive(Debug, Clone, PartialEq, Eq)]
pub struct ColouredSymbol {
    pub pos: Pos,
    pub colour: Colour,
}

#[derive(Debug, Clone, Copy, PartialEq, Eq)]
pub enum Colour {
    Black,
    White,
    Pink,
    Red,
    Orange,
    Yellow,
    Green,
    Turquoise,
    Blue,
    Purple,
}

I picked the list of colours based on the ones I remembered from the game. There are probably some missing, but it doesn’t really change the solver.

The puzzle model needs to keep track of which symbol is in each cell:

struct Cell<'ctx> {
    symbol: Option<Symbol>,
    region: z3::ast::Int<'ctx>,
}

#[derive(Debug, Clone)]
enum Symbol {
    Square(Colour),
    Sun(Colour),
}

impl<'ctx> PuzzleModel<'ctx> {
    ...
    fn add_squares(&mut self, squares: &[puzzle::ColouredSymbol]) {
        for s in squares {
            self.cell_mut(&s.pos).symbol = Some(Symbol::Square(s.colour));
        }
    }

    fn add_suns(&mut self, suns: &[puzzle::ColouredSymbol]) {
        for s in suns {
            self.cell_mut(&s.pos).symbol = Some(Symbol::Sun(s.colour));
        }
    }
    ...
}

Now, we can add constraints for these symbols!

We will need two helper vecs; one of squares and one of all symbols. These will contain colour and region of the symbols.

Then, we iterate over all the cells with symbols.

fn constrain_symbols(&self, solver: &z3::Solver) {
    let coloured_symbol_regions: Vec<_> = self
        .cell_positions()
        .iter()
        .map(|pos| self.cell(pos))
        .filter_map(|cell| match &cell.symbol {
            Some(symbol) => match symbol {
                Symbol::Square(colour) | Symbol::Sun(colour) => Some((colour, &cell.region)),
            },
            None => None,
        })
        .collect();
    let square_regions: Vec<_> = self
        .cell_positions()
        .iter()
        .map(|pos| self.cell(pos))
        .filter_map(|cell| match &cell.symbol {
            Some(Symbol::Square(colour)) => Some((colour, &cell.region)),
            _ => None,
        })
        .collect();
    for pos in self.cell_positions() {
        let cell = self.cell(&pos);
        match &cell.symbol {
            Some(symbol) => match symbol {
                Symbol::Square(colour) => ... // See below
                Symbol::Sun(sun_colour) => ... // See below
            },
            None => {}
        }
    }
}

For the squares, we ensure that every square with a different colour is in a different region:

Symbol::Square(square_colour) => square_regions
    .iter()
    .filter(|(colour, _)| *colour != square_colour)
    .for_each(|(_, region)| solver.assert(&region._eq(&cell.region).not())),

For the suns, we check that there are exactly two symbols with the same colour in the region - the sun itself, and one other.

Symbol::Sun(sun_colour) => {
    let same_colour_and_region = coloured_symbol_regions
        .iter()
        .filter(|(colour, _region)| colour == &sun_colour)
        .map(|(_colour, region)| region._eq(&cell.region))
        .collect::<Vec<_>>();
    solver.assert(&z3::ast::Bool::pb_eq(
        self.ctx,
        same_colour_and_region
            .iter()
            .map(|cond| (cond, 1))
            .collect::<Vec<_>>()
            .as_ref(),
        2,
    ));
}

Final thoughts

It should now be clear why an SMT solver like Z3 is a great way to solve complex constraint-based puzzles. Trying to implement a solver using traditional algorithmic approaches works in simple cases, but as the number of constraints grows, the complexity blows out massively.

For the sake of comparison, check out some of the existing solvers on the internet. They all have two things in common.

Firstly, they can’t solve any puzzle larger than 6x6.

Secondly, attempting to solve this puzzle will crash your browser:

This is not to fault the authors who wrote those solvers! It’s simply a task which Z3 excels at: quickly working out if something is solvable or not.

While a hand-coded solution might enumerate all the combinations from the start of the line to the end, Z3 has no concept of forwards or backwards, it simply reduces the problem down and eliminates impossibilities as it goes.

That’s it for part 2. Keep an eye out for part 3, where I will be taking a deep dive into “tetris” symbols.

If you enjoyed this post or have questions/thoughts, please leave a comment below!